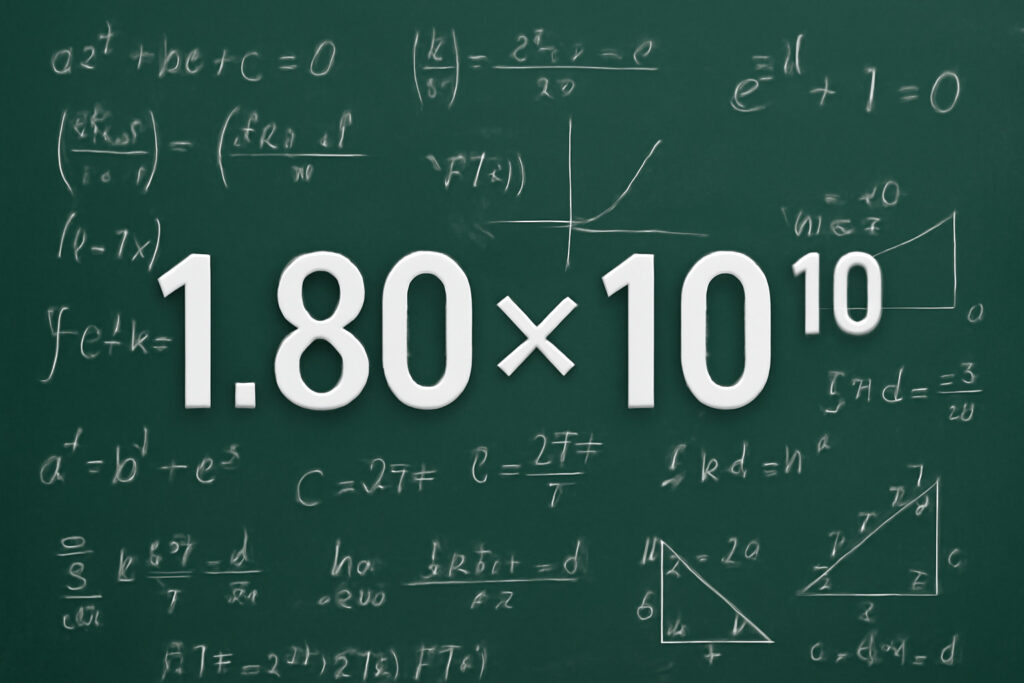If you’ve ever seen a number in a math problem that looks like 1.80E+10, you would probably ask yourself why that was written as such, what it means, and how it can be interpreted. This post wants to explain everything about 1.80E+10, what does it mean, some context about it, and how to operate with those numbers in several situations.
What Does 1.80E+10 Mean?
1.80E+10 is used to represent other very large or very small numbers more conveniently. In this notation:
- “E” is for “exponent” (as in ”times ten raised to the power of”).
- “1.80” is the base number.
- “+10” is the exponent.
Thus, 1.80E+10 translates to:
1.80 × 10¹⁰
Which means:
= 18,000,000,000 1.80 × 10,000,000,000 Substituting in the appropriate values, we get:
And yes, 1.80E+10 is another way to say 18 billion.
What is the point of using scientific notation, like 1.80E+10?
There are several advantages of using the scientific notation:
- Efficiency: It’d be silly to write and read 1.80E+10 as opposed to 18,000,000,000.
- Clarity: It decreases the possibility of mistakes in counting a long series of zeros.
- Universality: Researchers, engineers, and scientists across the globe get this format.
- Applications: Most programs automatically display very large numbers in scientific notation (Excel, calculators, and programming languages).
So in short, using scientific notation lets us express huge (or very small) numbers easily and accurately.
Where Is 1.80E+10 Used in Real Life?
Scientific notation is used for a variety of purposes in the sciences. Let me illustrate a few realistic scenarios where we might be dealing with the numbers like 1.80E+10:
Science and Astronomy
The distance between planets, the mass of stars and other astronomical measurements tend to be very large numbers. For example, the number of stars in a galaxy could easily be in the tens of billions.
Example:
- Amount of stars in a small galaxy: Approximately 1.80*10^10 stars.
Engineering
In electronics we are usually dealing with very large or very small numbers. Engineers perhaps could use scientific notation for electrical charges, frequencies, or data transfer rates.
Example:
- Amount of information carried by global Internet traffic every day: approximately 1.80E+10 bits.
Computing and Data Storage
With increasing data demand, we’re now sizing storage in gigabytes, terabytes, and even petabytes.
1 GB \(\approx 10^9\) bytes, so 18 GB could be written as 1.80E+10 bytes.
Finance and Economics
Some macroeconomic quantities like the total market capitalization of world markets (or national debts) can be expressed in scientific notation.
Example:
- A country’s GDP (in cents) might be represented as 1.80E+10 cents ($180 million).
How to Write 1.80E+10 in Standard Form
To convert 1.80E+10 to regular decimal number:
- Find the exponent: +10 indicates shifting the decimal 10 spaces to the right.
- From 1.80, move the decimal 10 places.
Step-by-step:
yaml
CopyEdit
1.80 → 18.0 → 180.0 → 1800.0 → 18000.0 → 180000.0 → 1800000.0 → 18000000.0 → 180000000.0 → 1800000000.0 → 18000000000.0
So, 1.80E+10 = 18 000 000 000.
How to Write 18,000,000,000 in Scientific Notation
Reversing the process:
- Move the decimal point after the first non zero number: 1.8000000000
- Count how many places you moved the decimal: 10 places.
- Thus 18,000,000,000 is converted to 1.80E+10.
Writers sometimes omit trailing zeros after the decimal if they’re not significant, but they keep them in 1.80 because it has two significant figures.
Scientific Notation in Calculators and Computers
If you are using calculators or computers:
- You might see 1.80E+10 at the beginning after inputting big numbers.
- Some systems automatically handle it when users input a very large or very small number.
Example using Excel:
- If I type 18000000000 into a cell, it may automatically be displayed as 1.80E+10 depending on how the cell is formatted.
In programming:
Languages such as Python or JavaScript use an “e” notation to similarly represent large numbers.
Example in Python:
python
CopyEdit
a = 1.80e10
print(a) # Output: 18000000000.0
Significant Figures in 1.80E+10
- 1*05+00_ASSY1DZT Measurement Conversion Table: 1.80E+10 Inches to Attometers Customize Values and click to convert.
- Sig figs indicate how precise a measurement is.
1, 3 significant figures, February 24, 1987 68M (68 mega) = 68,000,000 (fluctuated due to the difference between American and Great Britain definitions) (15 si, 15 sf) 1000 1,580 1.58E+3 In the given number – 1.80E+10, Let’s see what we have for significant figures: 1.80E+10 3 significant figures (1, 8 and 0)
Conclusion
It is a succinct and efficient way to express a very big number — 18 billion, to be exact. Being able to comprehend scientific notation like this is key to success across several fields, including science and engineering as well as finance and computing.
Once you can read, convert, and use numbers in scientific notation, you will be able to work with huge amounts or extremely small amounts of substances (maybe even in space) with ease, accuracy, and purpose. And whether you are solving astrophysics equations, tabulating financial data or writing software, the ability to work with values like these will make you a more literate and efficient computist.